김영준

Read, Think, Write

2 분 소요


앞에 3개의 포스트 내용은 선형 자료구조에 대한 개념 위주의 설명이었습니다.

사실상 오프닝이었고… 이번 포스트 부터 본편…! 알고리즘이 시작됩니다.

대망의 첫 알고리즘 포스트의 주인공은…😁

바로 누적합 알고리즘!


알고리즘이란…!

주어진 문제에 대해 ‘얼마나 효율적으로 해결할 수 있을까?’

를 고민해보는 것이라고 할 수 있죠.

그렇다면, 누적합 알고리즘은 어떤 상황에, 어떻게 적용해 볼 수 있는 아이디어인지!

천천히 알아봅시다.


1. 누적합 (Prefix Sum)

아래 이미지처럼 정수값이 담긴 배열에 1번 인덱스부터 3번 인덱스까지 구간의 합을 구한다고 가정해보죠.

배열1

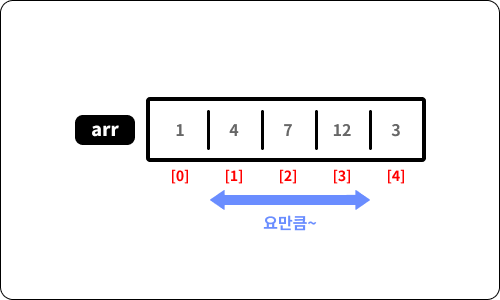
단순히 생각해본다면, 아래 코드처럼 반복문을 통해 합을 구해 볼 수 있을 것 같네요.

arr = [1, 4, 7, 12, 3]

start_idx = 1
end_idx = 3

result = 0

for i in range(len(arr)):
    if i >= start_idx and i <= end_idx:
        result += arr[i]

print(result)


그렇게 어려운 코드는 아니지만,

한번 가정을 해봅시다.

이러한 연산을 N번 반복한다면…? 배열의 길이가 엄청 길었다면…?

N번 만큼 구간의 합을 구하기 위해 엄~청 긴 배열을 매번 순회해야겠죠…

즉,

(구간의 합을 구하기 위해 순회하는 배열의 길이) x (구간합을 구하는 횟수 N)

만큼 반복이 될 겁니다…😂

비효율적인 코드인 것 같네요.


그래서 나온 아이디어가 바로, 누적합 알고리즘 입니다!

배열을 하나 새롭게 만들어두고 기존 배열의 0번 인덱스부터 n번 인덱스까지의 합을 담아두는 것이죠.

지금부터 새롭게 만들 이 배열을 누적합 배열(Prefix Sum)이라고 부르겠습니다.

그럼 한번 누적합 배열을 직접 만들어볼까요?


  • prefix_sum의 1번 인덱스의 값은 arr배열의 0번 인덱스부터 0번 인덱스까지의 합입니다.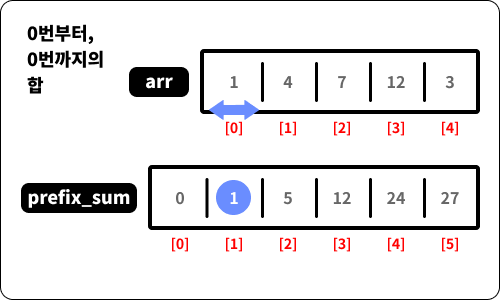

    누적합배열1

  • prefix_sum의 2번 인덱스의 값은 arr배열의 0번 인덱스부터 1번 인덱스까지의 합입니다.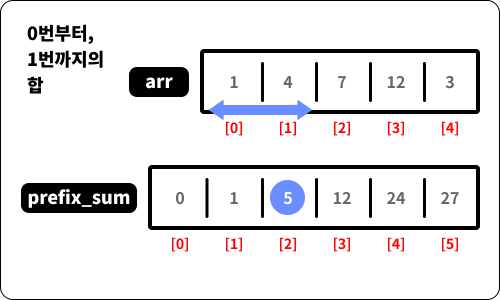

    누적합배열2

  • prefix_sum의 3번 인덱스의 값은 arr배열의 0번 인덱스부터 2번 인덱스까지의 합입니다.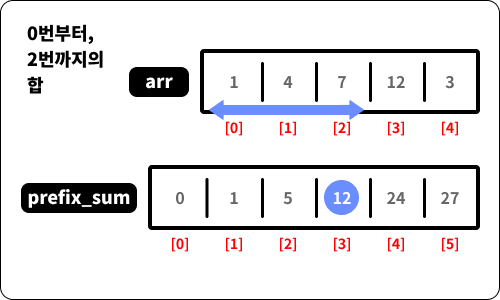

    누적합배열3

이런 식으로 반복한다면..

prefix_sum 의 n번째 인덱스에 들어가는 값은 arr의 0번부터 n-1번까지의 합이 담기게 됩니다.


그런데!

방금 누적합 배열을 만든 것 처럼,

prefix_sum의 n번째 인덱스에 값을 채워넣기 위해 매번 arr을 순회한다면,

조금이라도 반복을 줄이기 위해 누적합 알고리즘을 사용하는 의미가 줄어들겠죠?

이렇게 생각해봅시다.

  • prefix_sum[2]의 값은 arr[0]부터 arr[1]까지의 합입니다.
  • 그렇다면 prefix_sum[3]을 구할 때, 바로 한 칸 전 prefix_sum[2]와 arr[3]을 더한다면?

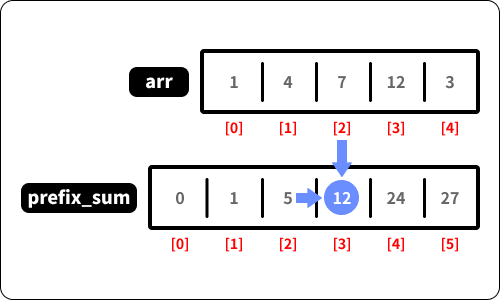
누적합배열5

이처럼, arr 배열을 매번 순회할 필요없이 한 칸 전의 prefix_sum의 값을 받아와서 간편하게 누적합 배열을 채울 수 있게 됩니다.

수식으로 정리해본다면,

prefix_sum[n] = prefix_sum[n-1] + arr[n-1] 이 되겠네요.


⚫ 연습 문제

그럼, 개념을 적용해볼 수 있는 문제를 하나 풀어보겠습니다.

해당 문제를 처음 보는 독자분들은 해당 링크를 천천히 읽어보시고,

적어도 30분은 어떻게 코드를 작성해볼지 구상해보는 단계를 꼭 거친 후에 포스트를 이어서 읽어주세요.

이 문제는 위의 개념을 그대로 적용해 볼 수 있기 때문에, 바로 문제를 풀어보겠습니다.

  • 변수에 값을 입력받습니다.

      N, M = map(int, input().split())
  arr = list(map(int, input().split()))

  • 정수 배열(arr)을 기반으로 누적합 배열(prefix_sum) 만듭니다.

    이 때, prefix_sum을 [0]으로 초기화 해줌으로써,
    prefix_sum[n] = prefix_sum[n-1] + arr[n-1] 수식상
    n이 1일 때, prefix_sum[n-1]를 무사히 연산할 수 있도록 해줍니다.

      perfix_sum = [0]

  for i in range(len(arr)):
      # 리스트의 내장함수 append() 를 활용
      perfix_sum.append(perfix_sum[i] + arr[i])

  • 구간의 합을 M번 출력합니다.

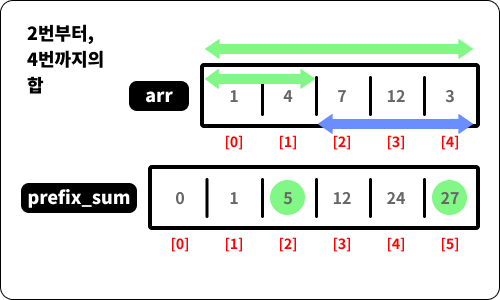
    누적합배열6

    예를 들어, 2번부터 4번까지의 합은, 0번부터 4번까지의 합에서 0번부터 1번까지의 합을 빼면 된다는 아이디어를 활용합니다. 위 그림처럼요.

      for _ in range(M):
      i, j = map(int, input().split())
      print(perfix_sum[j] - perfix_sum[i-1])


이제 전체 코드를 봐봅시다.

N, M = map(int, input().split())
arr = list(map(int, input().split()))

perfix_sum = [0]

for i in range(len(arr)):
    # 리스트의 내장함수 append() 를 활용
    perfix_sum.append(perfix_sum[i] + arr[i]) 

for _ in range(M):
    i, j = map(int, input().split())
    print(perfix_sum[j] - perfix_sum[i-1])


이렇게 오늘은 누적합 알고리즘의 개념과 예제 풀이까지 공부해봤습니다.

아래 누적합 알고리즘을 활용해 풀어볼 수 있는 문제의 링크를 달아놓았으니 참고해보셔요!

⚫ 더 연습해볼 수 있는 문제

  1. 백준 11660 구간합 구하기 5 » 링크
  2. 백준 21758 꿀따기 » 링크


댓글남기기

참고